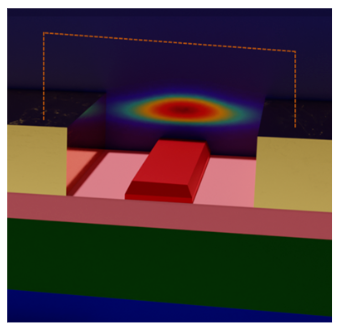
在這個示例中��,我們基于Mercante等人的工作[1]模擬了一種薄膜鈮酸鋰(LNOI)相位調制器。通過利用2023 R1.2版本引入的各向異性介電常數(shù)特性�����,我們在CHARGE中計算了由射頻引發(fā)的電容電場(E場)����。然后��,這些電場用于通過Pockels效應在電信波長下計算鈮酸鋰中的電光折射率擾動�。接著,我們在FEEM中計算了擾動的LN波導的光學模式�����,以及TE基模的電壓相關相位調制性能����,包括損耗和VπL。
光收發(fā)器將電信號轉換為光信號����。所有的計算都始于電子領域,然后通過將信號從電信號轉換為光信號���,我們可以提升更多的通道�����,擁有更大的帶寬�,這可以在長距離傳輸中顯著減小信號衰減。這些器件在互聯(lián)網(wǎng)的長距離傳輸中起著至關重要的作用���,以滿足流量和延遲需求的日益增長���。我們可以將光收發(fā)器及光電探測器視作連接到互聯(lián)網(wǎng)超級高速公路的出口和入口。
這些器件通常采用Mach-Zehnder干涉結構���,其中載波被分到兩個傳輸通道����,并在輸出處重新耦合��。通過施加有數(shù)據(jù)信息的電信號來改變兩個臂中的光的相位��,將導致在輸出處出現(xiàn)相干性��。Mach-Zehnder干涉結構通常用作非常敏感的光學儀器����,但在這種情況下,光的相位被有意地調制��,因此此類器件通常被稱為Mach-Zehnder調制器(MZM)����。當前,已經(jīng)使用了多種材料平臺和物理效應來實現(xiàn)這種功能�����。在這個示例中����,我們關注鈮酸鋰中的Pockel效應。
大多數(shù)用于相位調制的物理機制都比較弱���,導致器件整體需要非常大的尺寸�。另一方面�,一些特殊材料可能會導致傳輸損耗較大,或者難以與其它光學和電子集成�����。鈮酸鋰具有較大的吸收帶寬和明顯的各向異性,因此可以實現(xiàn)低損耗和高調制效率�。傳統(tǒng)的晶體鈮酸鋰已經(jīng)得到廣泛的應用,但是晶體鈮酸鋰的制備方法無法制備高折射率差的光波導�。最近在制備技術方面的發(fā)展使薄膜鈮酸鋰平臺成為超緊湊和高性能集成光子元件的極佳選擇。
在本文中�,我們展示了如何使用我們的有限元集成開發(fā)環(huán)境(IDE)來仿真鈮酸鋰薄膜光波導中的電光調制。本工作中進行的模擬包括兩個主要階段:電學和光學���。下面是所模擬的調制器的示意圖���。
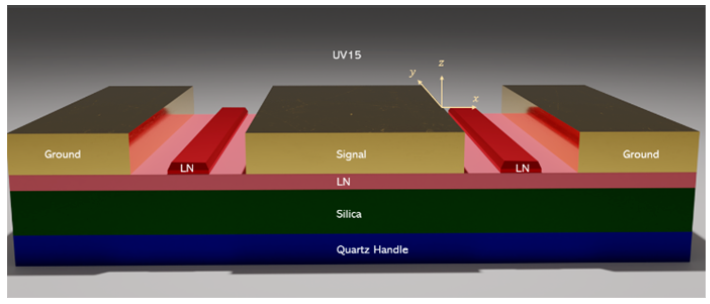
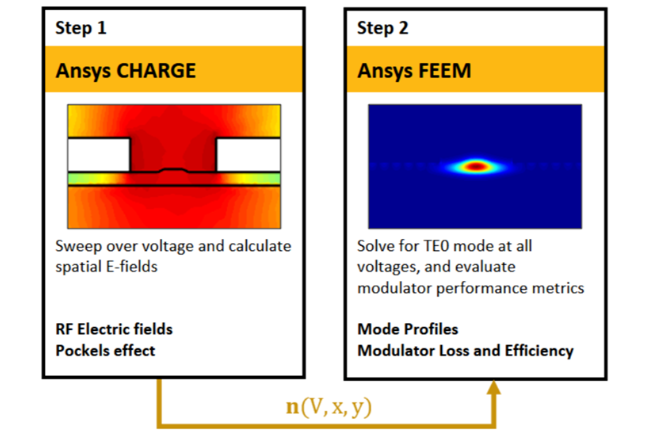
在步驟1中,我們使用CHARGE求解器來仿真施加電壓偏置后鈮酸鋰(LN)脊波導中的電場分布���。通過金電極以地-信號-地的配置施加電壓偏置���。信號電極上施加從0V到5V的電壓,間隔為0.5V�����。地電極上施加的電壓保持固定在0V�。所得電場結果將被用于通過Pockels效應計算LN材料中的折射率擾動。
在電學仿真中我們將得到以下結果:
靜電結果:靜電場數(shù)據(jù)集提供了許多數(shù)值��,包括CHARGE模擬的重要結果��,即電場(E場)在電容板之間的數(shù)值����。
電光折射率擾動:使用電場(E場)數(shù)值,經(jīng)計算可以得到施加電場后的的空間矢量折射率和所加電場導致的折射率差值�,其中折射率的變化dn如下圖所示。這兩個值將用于后續(xù)的光學仿真
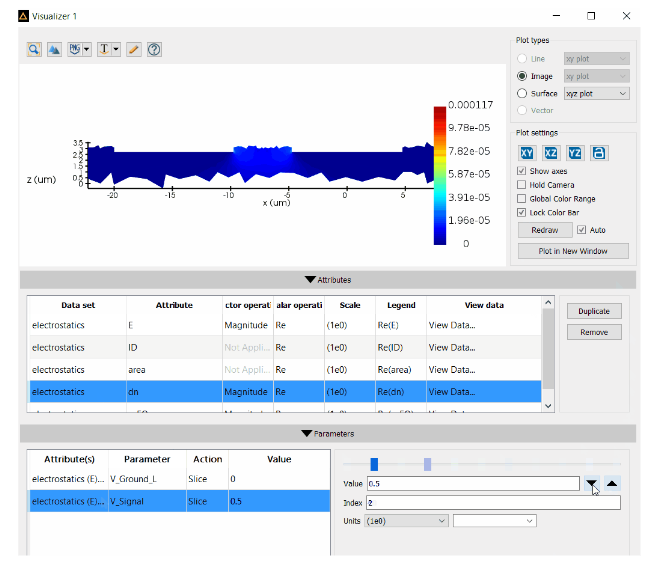
點擊圖片跳轉原文即可觀看動圖
根據(jù)步驟1中進行的折射率擾動計算��,創(chuàng)建了一個擾動nk材料模型��,并將其應用到LN波導結構中��。然后�,使用FEEM求解器來計算波長為1.55微米時波導中的模式。這些操作在一個for循環(huán)內(nèi)執(zhí)行�����,其中每次迭代對應一個電壓點����。我們通過掃描TE基模,并繪制有效折射率隨施加電壓的變化��。我們還計算相關的損耗(以dB/cm為單位)和不同電壓下的電壓-長度乘積 VπL。
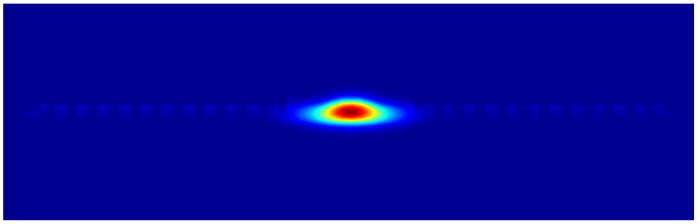
首先���,通過FEEM求解器�����,我們得到了在0-5V電壓下�����,LN脊波導的TE基模�。根據(jù)TE基模的模式輪廓��,發(fā)現(xiàn)在金屬電極下方出現(xiàn)了延伸的耗散尾巴�。需要注意的是,x-cut 的鈮酸鋰易于發(fā)生模式混合�,因為模式平面經(jīng)歷了兩種不同的折射率[2]。此外���,波導的TE模式和TM模式很可能與電介質-金電極界面上的等離子激元模式發(fā)生混合���,從而產(chǎn)生這些長的耗散尾巴。因此�����,我們使用FEEM仿真結果中的TE極化分數(shù)來仔細識別TE模式,認為大于極化分數(shù)95%的為TE模式���。
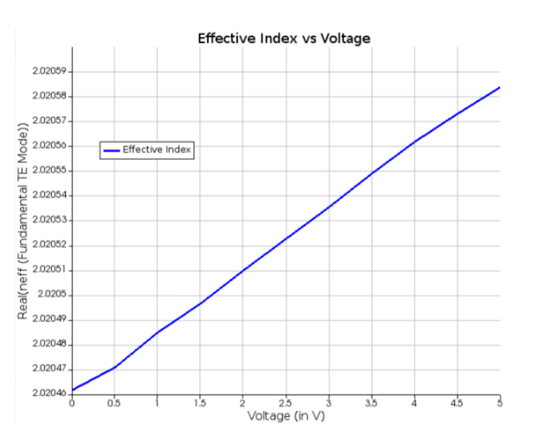
此外, TE基模的有效折射率是通過掃描電壓時�����,從FEEM所得的結果中收集的��。最終得到了下圖顯示的結果����,有效折射率與施加電壓為線性關系。
在不同電壓下�����,折射率的實部相對于0V時的折射率的發(fā)生了變化���。我們以Lπ作為度量參數(shù)����,表示產(chǎn)生π相位變化所需的調制波導長度。該值與電壓相乘以得到VπL���,是調制器性能的重要指標�����。用于計算Lπ的確切表達式如下:
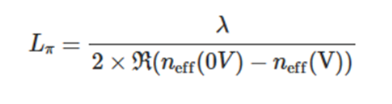
其中:
- Lπ是產(chǎn)生π相位變化所需的調制器長度��。
- λ 是波長��。
通過FEEM所得的數(shù)據(jù)�����,處理后得到了如下圖所示的關系曲線���。
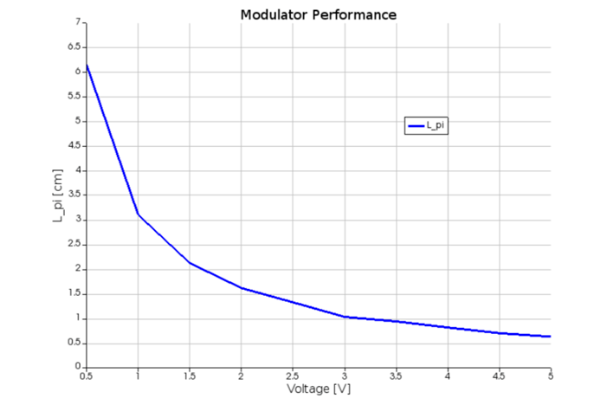
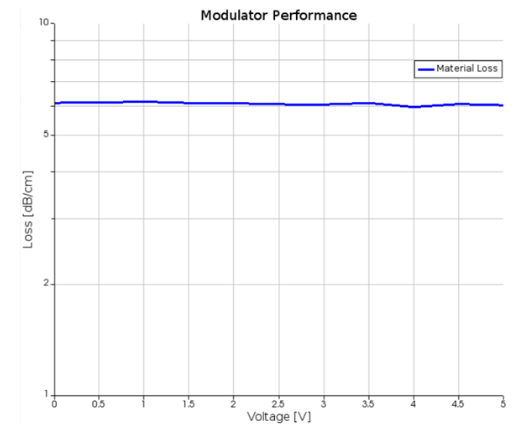
最后,F(xiàn)EEM還可以直接得到TE基模的損耗(以dB/cm為單位)���,如下圖所示��,調制器中的損耗幾乎在不同電壓下都保持穩(wěn)定�。這些損耗主要可以歸因于金電極����。因此�����,通過所得的關系曲線我們可以得出與其他調制器度量不同���,損耗不依賴于施加的電壓����。影響損耗的關鍵因素是電極之間的間距,可以優(yōu)化以獲得更好的性能與損耗比例�。
鈮酸鋰材料:CHARGE新功能
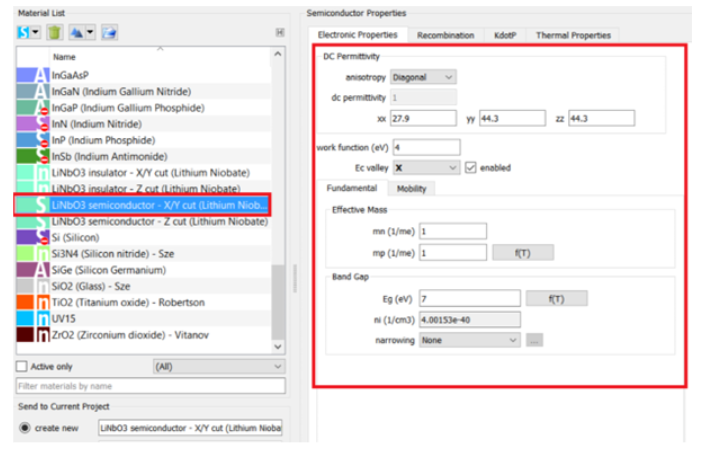
CHARGE Poisson求解器包括直流介電常數(shù)的對角各向異性,這是在2023 R1.2版本中添加到CHARGE求解器中的新功能����。在材料列表中,可以看到x/y-切割和z-切割的鈮酸鋰都可用作絕緣體和半導體類型的材料����。在本案例中使用的x-切鈮酸鋰在x軸上具有非凡的介電常數(shù)為27.9,在y軸和z軸上具有普通的介電常數(shù)為44.3����。
當將材料設置為絕緣體時���,它們在CHARGE模擬中被視為邊界條件。這在我們想要研究電荷傳輸時很有幫助���;然而���,我們大多數(shù)時候對靜電場感興趣,因此我們選擇半導體類型的材料��。在靜電場中���,泊松方程僅在半導體區(qū)域中求解��。鈮酸鋰的大能隙和可忽略的載流子濃度確保不會發(fā)生電荷傳輸���,只會使用靜電場計算。電極尖角周圍的邊緣效應會放大電場強度����。在實際制程中,不會存在類似的尖銳結構����,電極邊緣為弧形���,我們將看不到如此高的峰值電場。這不應該是一個重要的問題��,射頻場將對TE模式的有效折射率產(chǎn)生最大的影響���,主要集中在光模場的核心區(qū)域���。
參考文獻:
[1] Mercante, Andrew J., et al. "Thin film lithium niobate electro-optic modulator with terahertz operating bandwidth." Optics express 26.11 (2018): 14810-14816.
[2] Wang, Jingyi, et al. "Polarization coupling of X-cut thin film lithium niobate based waveguides." IEEE Photonics Journal 12.3 (2020): 1-10.
[3] Zhu, Di, et al. "Integrated photonics on thin-film lithium niobate." Advances in Optics and Photonics 13.2 (2021): 242-352.
翻譯:摩爾芯創(chuàng)-Bob